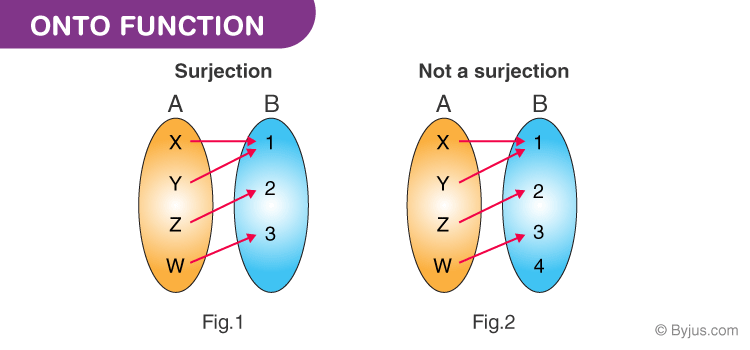
iopbusiness.blogg.se - Onto vs one to one graph

#ONTO VS ONE TO ONE GRAPH UPDATE#
#ONTO VS ONE TO ONE GRAPH FREE#

If $A$ is the standard matrix of $T$, then the columns of $A$ are linearly independent.

This definition applies to linear transformations as well, and in particular for linear transformations $T\colon \mathbb$.

$f$ is onto (or onto $Y$, if the codomain is not clear from context) if and only if for every $y\in Y$ there at least one $x\in X$ such that $f(x)=y$.

$f$ is one-to-one if and only if for every $y\in Y$ there is at most one $x\in X$ such that $f(x)=y$ equivalently, if and only if $f(x_1)=f(x_2)$ implies $x_1=x_2$.

"One-to-one" and "onto" are properties of functions in general, not just linear transformations.ĭefinition. T maps $T: \mathbb R^n$ onto $\mathbb R^m $ iff the columns of A span $\mathbb R^m $. Let $T: \mathbb R^n \to \mathbb R^m $ be a linear transformation and let A be the standard matrix for T. Then there is this bit that confused be about onto:

$\mathbb R^m $ is the image of at most one x in $\mathbb R^n $Īnd then, there is another theorem that states that a linear transformation is one-to-one iff the equation T(x) = 0 has only the trivial solution. $T: \mathbb R^n \to \mathbb R^m $ is said to be one-to-one $\mathbb R^m $ if each b in $\mathbb R^m $ is the image of at least one x in $\mathbb R^n $ $T: \mathbb R^n \to \mathbb R^m $ is said to be onto $\mathbb R^m $ if each b in

#ONTO VS ONE TO ONE GRAPH UPDATE#

I'll check back after class and update the question if more information is desirable. The task is determine the onto/one-to-one of to matrices) And I don't want to get a ban from uni for asking online.

(Sorry for not posting the given matrix, but that is to specific.

#ONTO VS ONE TO ONE GRAPH FREE#

Would a zero-row in reduced echelon form have any effect on this? I just assumed that because it has a couple of free variables it would be onto, but that zero-row set me off a bit. Compute answers using Wolframs breakthrough technology & knowledgebase, relied on by millions of students & professionals. The definition of onto was a little more abstract. Is x3 - x one-to-one and onto Natural Language Math Input Extended Keyboard Examples Upload Random. If the vectors are lin.indep the transformation would be one-to-one. The definition of one-to-one was pretty straight forward. This says that, for instance, R 2 is “too small” to admit an onto linear transformation to R 3. Each row and each column can only contain one pivot, so in order for A to have a pivot in every row, it must have at least as many columns as rows: m ≤ n. The matrix associated to T has n columns and m rows. If T : R n → R m is an onto matrix transformation, what can we say about the relative sizes of n and m ? Tall matrices do not have onto transformations

Of course, to check whether a given vector b is in the range of T, you have to solve the matrix equation Ax = b to see whether it is consistent. To find a vector not in the range of T, choose a random nonzero vector b in R m you have to be extremely unlucky to choose a vector that is in the range of T. Whatever the case, the range of T is very small compared to the codomain. This means that range ( T )= Col ( A ) is a subspace of R m of dimension less than m : perhaps it is a line in the plane, or a line in 3-space, or a plane in 3-space, etc. Suppose that T ( x )= Ax is a matrix transformation that is not onto. The previous two examples illustrate the following observation. Note that there exist tall matrices that are not one-to-one: for example,Įxample (A matrix transformation that is not onto) This says that, for instance, R 3 is “too big” to admit a one-to-one linear transformation into R 2. Each row and each column can only contain one pivot, so in order for A to have a pivot in every column, it must have at least as many rows as columns: n ≤ m. If T : R n → R m is a one-to-one matrix transformation, what can we say about the relative sizes of n and m ? Wide matrices do not have one-to-one transformations If you compute a nonzero vector v in the null space (by row reducing and finding the parametric form of the solution set of Ax = 0, for instance), then v and 0 both have the same output: T ( v )= Av = 0 = T ( 0 ). All of the vectors in the null space are solutions to T ( x )= 0. This means that the null space of A is not the zero space. By the theorem, there is a nontrivial solution of Ax = 0. Suppose that T ( x )= Ax is a matrix transformation that is not one-to-one. The previous three examples can be summarized as follows. Hints and Solutions to Selected ExercisesĮxample (A matrix transformation that is not one-to-one).

3 Linear Transformations and Matrix Algebra